게임수학 [2장 대수학과 방정식]
대수학과 방정식
게임에 기본적으로 알고 있는 수학의 개념을 넣는다고 할 때 가장 중요한 부분이라고 한다.
이러한 개념들이 게임에서 어떻게 동작하는지 알아본다..!
대수학
수학이 머리가 아플 땐 게임으로 생각하면 쉽게? 이해할 수 있다.
재밌게가 맞는 것 같다..
간단한 로켓게임을 만든다고 했을 때, 내부적으로 사용하는 변수값들을 가지고 방정식을 만들어서 다양한 값을 도출해낼 수 있다.
- 로켓이 가질 수 있는 최대 용량의 연료 Max_Fuel 변수명 m
- 로켓이 초당 태우는 연료의 양 Burn_Rate 변수명 b
- 로켓의 현재 연료량 Curr_Fuel 변수명 c
- 로켓이 날아다니는 시간 tim 변수명 t
최대 연료가 100이며 초당 2의 연료를 태운다고 했을 때 최대 몇로를 날아다닐 수 있는지 구하는 방법은 간단하다.
단순 계산으로 50초라는 시간이 나오지만 방정식으로 나타내면 식으로 게임에 적용할 수 있다.
현재 연료(0) = 최대 연료(100) - (초당 연료(2) * 시간 (0))
c = m - (b * t)
이런 식으로 전개된다.
그렇다면 로켓이 10초 동안 날게 되면 현재 연료는 몇일까? 라는 의문에는 위의 식에 대입해보면서 직접 결과를 확인할 수 있다.
코드로는 매우 빠르게 위 공식을 사용해 값이 도출된다.
c = 100 - (2 * 10)
c = 80
진짜로 이 코드 게임에 적용한다면 최대 최소에 대한 예외정도만 추가해주면 될 것 같다.(clamp를 사용해서..?)
반대로 최대로 날아다닐 수 있는 시간을 구하는 방정식으로 변경한다고 한다면
0 = 100 - (2 * t)
t = 50
이며 방정식으로 표한하면
\[t = \frac{c - m}{-b}\]
다른 값들을 메인으로 한 방정식도 다양하게 만들 수 있으며 실제로 적용하여 수학로직으로서 사용 가능하다..!
부등식
위 예제를 그대로 활용해서 C(현재 연료량)은 0~M(최대 연료량)에 속하게 된다.
Math클래스 함수의 Clamp를 활용하면 코드상으로 쉽게 최소, 최대 값을 제한할 수 있다.
\[0 <= c <= m\]
if(0 <= c && c <= m) 처럼 if로도 가능하다.
그렇다면 방정식의 이항과 부등식의 이항의 차이점은 뭘까
바로 방정식 자체를 뒤집어야 한다는 점이다.
\[(t = 50) == (50 == t)\]
\[(c >= 50) != (c <= 50)\]
양변에 값 연산을 하는 방법은 다음과 같다.
\(10 >= -2x + 5\) \(5 >= -2x\) \(\frac{5}{-2} <= x\)
음수를 양변에 곱하거나 나눌 땐 부호가 뒤집힌다.
그래프
그래프는 값들 사이에 연관성을 조사할 때 자주 사용된다.
t(시간), c(현재 연료)의 값으로 그래프를 그린다고 할 때 독립변수를 가로 축에 두는 경우가 많다.
따라서 값을 따로 조절할 수 없는 종속 변수들은 세로축에 두어서 변화를 관찰한다.
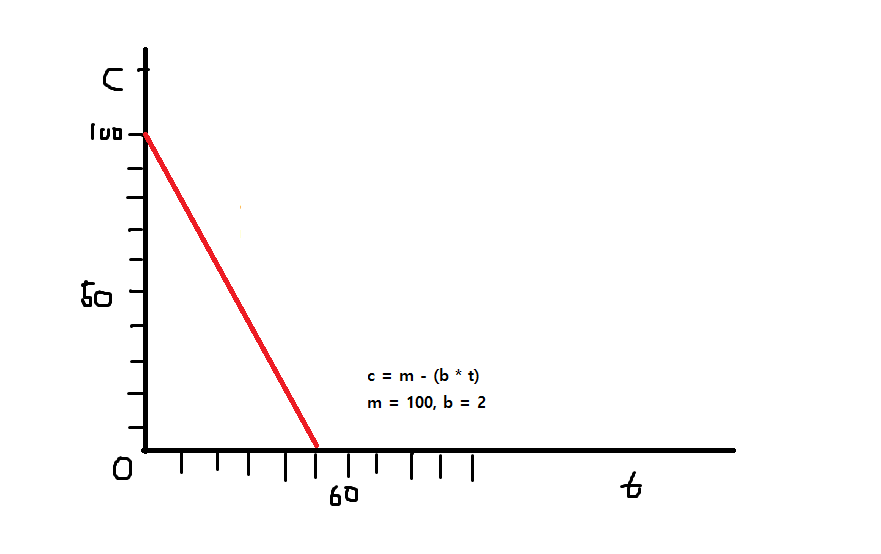
그래프를 그리면 좋은 점은 보간을 활용할 수 있다는 점이다.
원하는 값을 바로 바로 알아 볼 수 있기 때문에 쉽게 알 수 있다.
math클래스 함수에서는 Lerp라는 함수로 제공해준다.
기울기와 절편
Lerp함수를 통해 선형그래프의 절편들을 알아낼 수 있다.
Vector2.Lerp함수를 통해서도 알아낼 수 있다.
기울기를 쉽게 알 수 있는 방식을 소개해준다.
\[slope = \frac{Rise}{Run}\]
그래프가 있다면 위의 방법을 활용해서 두 절편사이의 rise즉 -y축의 길이를 run은 x축의 길이를 넣어주면 해당 기울기를 알 수 있지만 계산식으로는 더욱 높은 정확도로 구할 수 있다.
\[\frac{(y_2 - y_1)}{(x_2 - x_1)}\]
위에서 그린 그래프의 기울기는 -2즉 기울기임을 알 수 있다.
선형 방정식
지금까지 배운 방정식은 모두 선형방정식이다.
\[y = mx + c\]
위의 식을 현재 연료를 계산하는 식에 그대로 적용해본다.
y는 y축 즉 c x도 마찬가지로 t를 의미, m은 기울기를 뜻한다.
앞서 기울기가 -2였기 때문에 음수로 표시하고 c는 상수항을 더 해준다.(100)
\[c = -(bt) + m\]
식을 선형방정식에 맞게 정리해보니 결국 부등식에서 정리한 식과 같아졌음을 알 수 있다.
선형방정식의 핵심은 x이다. 위에서 사용된 x에 곱하기만 사용했기 때문이다.
제곱이나 루트를 씌운다면 곡선의 형태를 띄게 된다.
절편을 살펴봐도 일정한 비율로 값이 증가 된다면 선형이라고 생각할 수 있다. ex) x축은 2씩 증가 y축은 1씩증가한다면

댓글남기기