알고리즘 [이중연결 리스트 && 이진트리]

1. 🔎 우선순위 큐

우선순위 큐는 데이터 구조의 일종임.

데이터구조는 여러개의 데이터항목을 저장하는 구조체

우선순위 큐 ADT(Abstract data type / 추상자료형)
인간에게 친숙한 데이터구조형태이다 -> 추상자료형

각 항목은 키와 원소가 쌍으로 이루어짐
키는 대체로 단단한 것들 EX)주민번호, 이름, 알파벳 등등

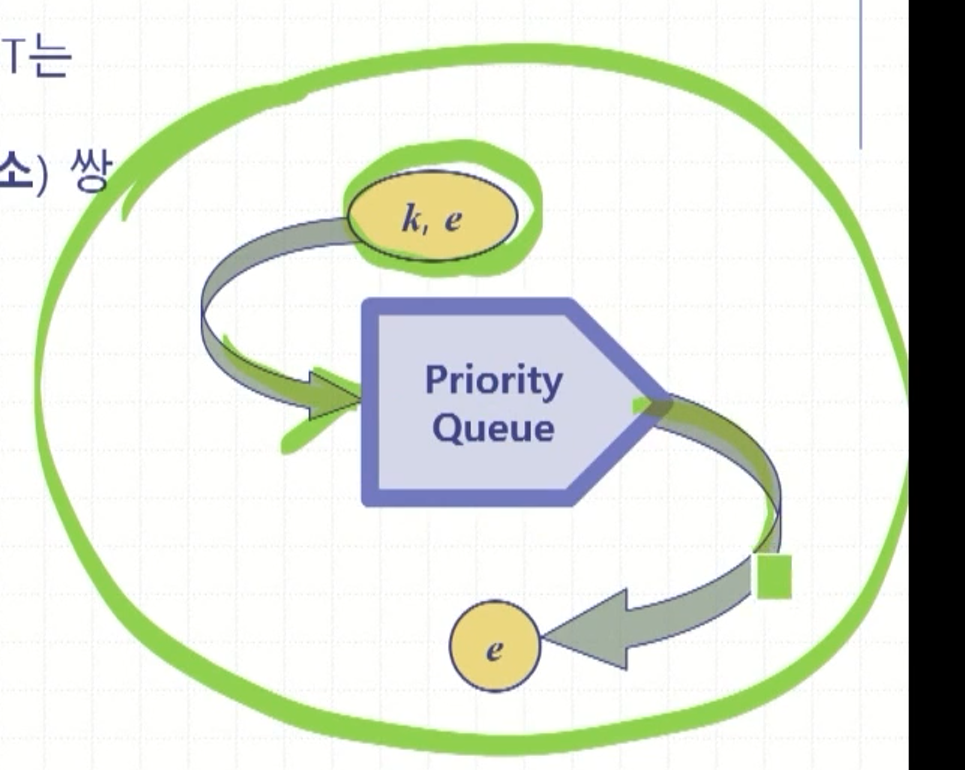
사용하는 키값을 넣고 그에 해당하는 원소값을 반환받음

큐를 사용한 예 )

1. 주식시장
2. 탑승 대기자 (키: 예약시간 / 원소: 자리 )
3. 옥션 (키: 사는 가격 / 원소: 구매자 이름)

ADT를 살펴보자.

1.1. 메서드

• insertitem(k,e): 키 k인 원소 e를 큐에 삽입
• element removeMin(): 큐로부터 최소 키를 가진 원소를 삭제하여 반환 (최소 시간, 최소 가격 매수 등 알고리즘에 사용, Max일수도 있음, 큐의 원소 반환 메소드)
• integer size(): 큐의 항목수를 반환
• boolean isEmpty(): 큐가 비어 있는지 여부를 반환
• element minElement(): 큐에서 최소 키를 가진 원소를 반환 (접근 메서드)
• element minkey(): 큐에서 최소 키를 반환 (접근 메서드, 키값 반환!!)
• emptyQueueException(): 비어있는 큐에 대해 삭제나 원소 접근을 시도할 경우 발령
• fullQueueException(): 만원(꽉찬) 큐에 대해 삽입을 시도할 경우 발령

1.2. 우선순위 큐를 이용한 정렬

1. 연속적인(반복) insertitem(e,e)작업을 통해 원소들을 하나씩 삽입 (key == e 로 전제) 높이 그자체를 원소로 사용 (e = 2.7 길이 입력 즉, 키,값이 둘다 2.7)
2. 연속적인(반복) removeMin()작업을 통해 원소들을 정렬 순서로 삭제 즉, 반환

의사코드

Alg PQ-Sort(L)    //Priority Queuing - sort 즉 우선순위 큐 정렬 알고리즘
 input list L            //정렬하라고 주어진 리스트 list L
 output sorted list L    //출력 리스트

1. P <- empty priority queue //비어있는 제2의 공간 (P: 비어있는 큐)
2. while (!L.isEmpty())      //처음 L의 리스트가 비어있지 않다면
  e <- L.removeFirst()     //첫번째 원소를 삭제하여 e라고 부른다.(대입)
  P.insertItem(e)          //큐 P에 e의 값을 넣는다.
3. while (!P.isEmpty())      //P가 비어있지 않는동안(반복)
  e <- P.removeMin()       //제일 작은 값을 e에 대입
  L.addLast(e)             //리스트 맨뒤에 삽입(즉 맨 왼쪽 부터 삽입)
4. return                    //반환

여기서 사용한 자료구조는 큐, 리스트 사용

실행시간은 우선순위 큐의 구현에 따라 다르다.

안의 메서드 삽입,삭제,접근(ex. removeMin)이 전부 상수의 시간이 걸린다는 가정하에 선형시간이 걸린다 0(n).

하지만 메서드들이 반복문이기 때문에 위처럼 0(n)는 가능하지 않다.

L,P는 일반(generic)적인 알고리즘이다. 즉, 배열이나 연결리스트로 선언해도 가능하다.

앞으로도 알고리즘을 작성할 때 일반이 가능하도록 작성하는 것이 좋다.

1.3. 리스트에 기초한 우선순위 큐

• 무순리스트로 구현
  insertitem: O(1) 시간 소요 - 항목을 리스트의 맨앞 또는 맨뒤에 삽입할 수 있음 removeMin,minKey,minElement: O(n) 시간 소요 - 최소 키를 찾기 위해 전체 리스트를 순회해야 하므로

• 순서리스트로 구현
  insertitem: O(n) 시간 소요 - 항목을 삽입할 곳을 찾아야 하므로 removeMin,minKey,minElement: O(1) 시간 소요 - 최소 키가 리스트의 맨앞에 있으므로

알고리즘의 소요시간을 적을 때 가장 최악의 성능을 생각하고 적어야함

무순리스트로 구성한 정렬한 알고리즘을 선택정렬이라고 부르고 순서리스트로 구성한 정렬 알고리즘은 삽입정렬이라고 부른다.

• 선택정렬(selection-sort)
  PQ-sort의 일종, 우선순위 큐를 무순리스트로 구현한다.
  실행시간 insertitem작업을 사용하여 원소들을 우선순위 큐에 삽입하는데 O(n)시간 소요 - 리스트에서 큐로 이동 removeMin작업을 사용하여 원소들을 우선순위큐로부터 정렬 순서로 삭제하는데 다음에 비례하는 시간 소요 - 큐에서 리스트로 이동(큐에선 삭제) n+(n-1)+(n-2)+…+2+1 total -> O(n²)

• 삽입정렬(insertion-sort)
  PQ-sort의 일종, 우선순위 큐를 순서리스트로 구현
  실행시간
  insertitem작업을 사용하여 원소들을 우선순위 큐에 삽입하는데 다음에 비례하는 시간 소요 0+1+2+…+(n-2)+(n+1)+n
  removeMin작업을 사용하여 우선순위큐로부터 정렬 순서로 삭제하는데 O(n) 시간 소요 total -> O(n²)

1.4. 제자리 수행 (예습)

선택정렬, 삽입정렬 둘다 O(n)의 공간을 차지하는 외부의 우선순위 큐를 사용하여 리스트를 정렬하기 때문에 상대적으로 많은 메모리를 차지한다.

이때 리스트 자체의 공간만 사용한다면 O(1)이며 이것을 제자리(in-place)에서 수행한다고 말한다.

어떤 정렬 알고리즘이 정렬 대상 개체를 위해 필요한 메모리에 추가하여 오직 상수 메모리만을 사용한다면, 제자리에서 수행한다고 한다. ex) 버블 정렬

제자리 선택정렬(selection-sort)가 외부의 데이터구조를 사용하는 대신 제자리에서 수행하도록 구현하려면 리스트 앞부분을 정렬상태로 유지, 리스트를 변경하지 않고 swap을 사용

제자리 삽입정렬(insertion-sort)가 외부의 대이터구조를 사용하는 대신, 제자리에서 수행가능하도록 구현하려면 리스트 앞부분을 정렬상태로 유지, 리스트 상태를 변경하는 대신 AR[n+1] <- AR[n]사용

제자리 정렬 알고리즘

Alg inPlaceSelectionSort(A)
 input array A of n keys
 output sorted array A

1. for pass <- 0 to n – 2
  minLoc <- pass
  for j <- (pass + 1) to n – 1
   if (A[j] < A[minLoc])
    minLoc <- j
  A[pass] <-> A[minLoc]
2. return

Alg inPlaceInsertionSort(A)
 input array A of n keys
 output sorted array A

1. for pass <- 1 to n – 1
  save <- A[pass]
  j <- pass – 1
  while ((j >= 0) & (A[j] > save))
   A[j + 1] <- A[j]
   j <- j – 1
  A[j + 1] <- save
2. return

1.4.1. 공통점

1. 두개의 정렬 모두 전체적으로 O(n²)사용(간단하게 반복문 두개!)
2. 구현이 단순하다.
3. 제자리 버전은 공간 O(1) 소요
4. 작은 n에 대해 유용하다

1.4.2. 차이점

1. 초기리스트가 완전히 또는 거의 정렬된 경우 제자리 삽입정렬이 더 빠르다. (내부 반복문 즉, 삽입시 정렬할때 O(1)시간이 소요 따라서 전체적으로 O(n)시간 소요)
2. A[j + 1] <- A[j] 작업이 비싼 경우 제자리 선택정렬이 빠르다. 작업이 패스마다 O(1)시간이 수행되는 반면에 제자리 삽입정렬은 최악의 경우 O(n)이 소요된다.

• 복잡도를 계산할 때는 항상 최악을 생각하기! 필요에 따라 선택정렬, 삽입정렬을 생각해야함

우선순위 큐	insertItem	removeMin	minKey,minElement	정렬방식
무순리스트	O(1)	O(n)	O(n)	선택 정렬
순서리스트	O(n)	O(1)	O(1)	삽입 정렬

내생각엔.. 많은 비교연산이 계속해서 필요하다면 당연하게 삽입정렬을 사용할 것 같다..

++ 성능요약부분 강의 듣고 정리

2. 이중연결리스트(Doubly Linked List) - 복습

우선 이중연결 리스트를 이해하기 위해서는 Linked List 즉, 단순연결리스트를 이해해야 한다.

단순연결 리스트는 노드에 next라는 포인터변수만 존재하였는데 이중연결 리스트는 새로운 포인터 변수가 하나 더 필요하다.

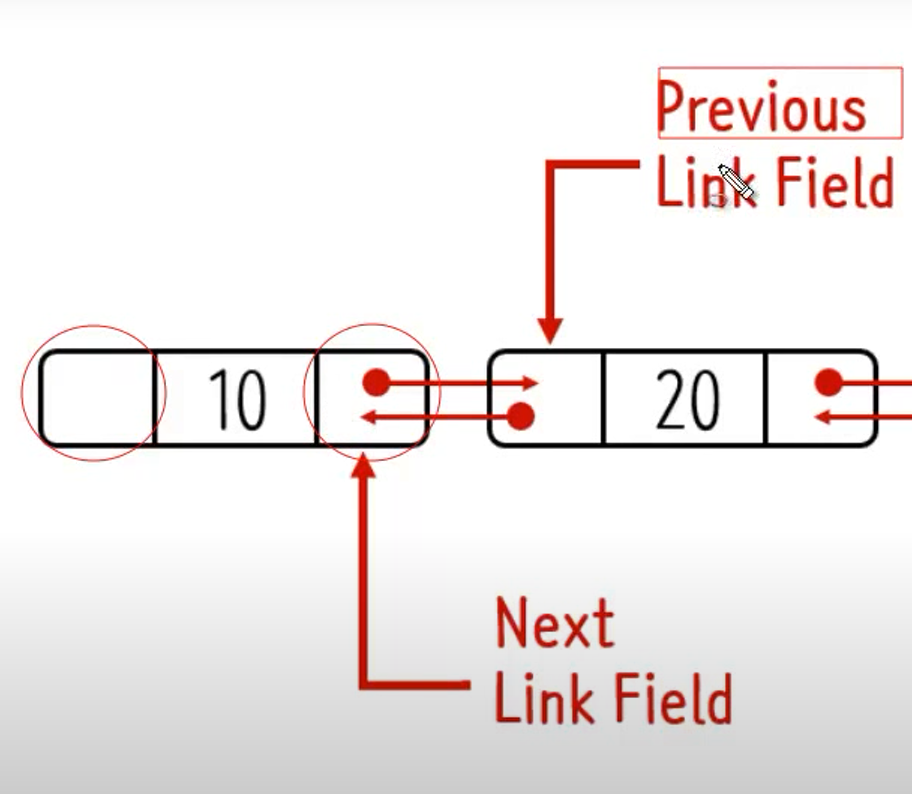
가장 큰 차이점이자 장점이 바로 이전 노드를 가르키는 변수와 다음노드를 가르키는 변수가 존재한다는 것이다.

• 장점: get(1)이라는 함수를 실행했을 때 리스트상에서 인덱스 값이 1이니 왼쪽에서 탐색하는 것이 빠르다. 그렇다면 get(123123)이라면 왼쪽부터 탐색한다면 탐색시간이 길어질 것이다.
  하지만 이중연결리스트는 오른쪽부터 탐색또한 가능하기 때문에 탐색시간이 적다는 장점이 있다.(이전 노드를 가리키는 변수가 존재) 리스트의 길이를 절반으로 나눠 적다면 next를 통해 탐색하고 많다면 prev를 통해 탐색한다.

• 단점: 위에서 말한 장점이 바로 단점이 된다. 하나의 포인터 변수를 선언하기 때문에 메모리를 더 잡아먹게 되고 조금 더 복잡하다는 단점이 있다.

2.1. 실습(C언어)

이중연결리스트를 간단하게 구현해봤다.

메서드

• add: 원하는 위치에 노드 추가
• del: 원하는 위치 노드 삭제
• print: 리스트 값 출력
• get: 원하는 위치 노드 값 출력

각 입력에 대한 예외 처리는 순위를 벗어날 때만 구현..

#define _CRT_SECURE_NO_WARNINGS //scanf오류 무시

#include <stdio.h>
#include <stdlib.h>
//표준라이브러리 선언

struct NODE { 
    struct NODE* prev;
    char elem;
    struct NODE* next;
}; //이중연결리스트 노드 구조체

struct double_list {
    struct NODE* head;
    struct NODE* tail;
    int size;
};// 이중연결리스트 구조체

//함수 선언부
void init();
void add(struct double_list* List);
void print(struct double_list* List);
void del(struct double_list* List);
void get_char(struct double_list* List);

//프로그램 시작점
int main() {

    int n;
    char a; //입력받을 변수 선언
    struct double_list* List; //리스트 선언 후 동적할당
    List = (struct double_list*)malloc(sizeof(struct double_list));

    init(List); // 초기화

    scanf("%d", &n);
    getchar(); //enter키 먹음

    while (n)
    {
        scanf("%c", &a);
        getchar();

        if (a == 'A')
        {
            add(List);
        }
        else if (a == 'D')
        {
            del(List);
        }
        else if (a == 'G')
        {
            get_char(List);
        }
        else if (a == 'P')
        {
            print(List);
        } 
        n--;
    }

    return 0;
}

//이중연결리스트 초기화 부분
void init(struct double_list * List)
{
    struct NODE * header = (struct NODE*)malloc(sizeof(struct NODE)); //메모리 동적할당 및 머리,꼬리노드 생성
    struct NODE * trailer = (struct NODE*)malloc(sizeof(struct NODE));

    header->prev = NULL;
    trailer->next = NULL;

    header->next = trailer;
    trailer->prev = header; // 노드끼리 연결

    List->head = header;
    List->tail = trailer; //리스트에 꼬리 머리 노드 연결

    List->size = 2;
}

void add(struct double_list* List)
{

    int r;
    char e;

    scanf("%d %c", &r,&e); //값 입력받음
    getchar(); //enter키 먹음

    if ((List->size)-1 < r) //예외 처리 여기서 -1인 이유는 노드 추가이기 때문에 추가된 길이 생각해서
    {
        printf("invalid position\n"); 
        return; // 중요!! 아무 처리하지 않고 넘어갈려면 return
    } 

    struct NODE* cur = List->head; //탐색 노드 선언
    
    for (int i = 0; i < r-1; i++)
    {
        cur = cur->next;
    } // r, 즉 삽입하고 싶은 순위의 전 노드까지

    struct NODE* newnode = (struct NODE*)malloc(sizeof(struct NODE)); //새로운 노드 생성
    newnode->elem = e; //값 입력

    struct NODE *temp, *temp1; // 두가지 임시 구조체 포인터 변수 생성

    temp = cur;
    temp1 = cur->next;
    //임시 노드 저장

    temp->next = newnode;
    newnode->prev = temp;

    temp1->prev = newnode;
    newnode->next = temp1;
    // 차례대로 노드 연결

    List->size++; //사이즈 증가
}

void del (struct double_list* List)
{
    int r;
    scanf("%d", &r);
    getchar();

    if ((List->size) - 2 < r) //예외 처리 여기서 -2인 이유는 꼬리 머리 노드 제외하고 생각
    {
        printf("invalid position\n");
        return; // 중요!! 아무 처리하지 않고 넘어갈려면 return
    }

    struct NODE* cur = List->head; //탐색 노드 선언

    for (int i = 0; i < r; i++)
    {
        cur = cur->next;
    } // r, 즉 삭제하고 싶은 순위 노드까지

    struct NODE* temp, * temp1; // 두가지 임시 포인터 생성

    temp = cur->prev; //삭제하고 싶은 노드 앞뒤 노드 가리킴
    temp1 = cur->next;

    temp->next = temp1; //서로 연결
    temp1->prev = temp;

    free(cur); //삭제(필수!)
    
    List->size--;
}

void get_char(struct double_list* List)
{
    int r;
    scanf("%d", &r);
    getchar();

    if ((List->size) - 2 < r) //예외 처리
    {
        printf("invalid position\n");
        return; // 중요!! 아무 처리하지 않고 넘어갈려면 return
    }

    struct NODE* cur = List->head; //탐색 노드 선언

    for (int i = 0; i < r; i++)
    {
        cur = cur->next;
    }

    printf("%c\n", cur->elem);
}

void print(struct double_list* List)
{
    struct NODE* cur = List->head;

    for (int i = 0; i < (List->size) - 2; i++)
    {
        cur = cur->next;
        printf("%c", cur->elem);
    }
    printf("\n");
}

다시 복습하면서 공부하니 확실하게 이해가 된다.

중간 중간 조금 더 가독성 좋게 코딩을 할 수 있지만 일단 이해를 해야해서…

예를 들어 삽입은 다른 임시노드를 생성하지 않고 가능하다고 하는데 일단 삭제와 삽입을 비슷한 형태로 만들어보고 싶어서 이렇게 코딩했다.

3. 트리(tree) - 복습

트리 관련 용어

• 루트노드(root node): 부모가 없는 최상위 노드
• 단말노드(leaf node): 자식이 없는 노드
• 크기(size): 트리에 포함된 모든 노드의 개수
• 깊이(depth): 루트 노드부터의 거리
• 높이(height): 깊이 중 최댓값
• 차수(degree): 각 노드의 (자식 방향) 간선 개수

기본적으로 트리의 크기가 N일 때, 전체 간선의 개수는 N-1개이다.

3.1. 이진 탐색 트리(Binary Search Tree)

이진 탐색이 동작할 수 있도록 고안된 효율적인 탐색이 가능한 자료구조의 일종이다.

이진 탐색 트리는 왼쪽 자식 노드 < 부모 노드 < 오른쪽 자식 노드<

부모노드보다 왼쪽 자식노드가 작고 부모노드보다 오른쪽 자식노드가 크다.

여기서 14의 값을 찾고자 한다면 맨 처음 루트노드에서 14는 10보다 크기 때문에 오른쪽 노드로 이동한다.

17은 14보다 크기 때문에 왼쪽으로 이동한다.

이렇게 방문하다 보면 14의 값을 찾을 수 있다.

이진탐색트리는 트리의 자료구조의 하나로 이상적인 탐색속도를 낼 수 있다.(이진탐색트리로 균형이 맞춰져 있다는 가정하에 log(n))

3.2. 트리의 순회(Tree Traversal)

트리 자료구조에 포함된 노드를 특정한 방법으로 한 번씩 방문하는 방법을 의미.

• 전위 순회(pre-order traverse): 루트를 먼저 방문합니다.
• 중위 순회(in-order traverse): 왼쪽 자식을 방문한 뒤에 루트를 방문합니다.
• 후위 순회(post-order traverse): 오른쪽 자식을 방문한 뒤에 루트를 방문합니다.

3.3. 실습(C언어)

#define _CRT_SECURE_NO_WARNINGS

//표준라이브러리 선언
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

//이중연결리스트 노드 생성
typedef struct node 
{
 int data;
 struct node* right;
 struct node* left;
}node;

//함수 선언부
void add_node(node* L);
void search(node* L);

//프로그램 시작점
int main()
{
 int n, m;
 node* tree; //뿌리 노드를 가리키게 할 포인터 변수

 scanf("%d", &n);
 getchar();

 int x, y, z;
 scanf("%d %d %d", &x, &y, &z);
 getchar();

 node* rootnode; //뿌리 노드 동적 생성
 rootnode = (node*)malloc(sizeof(node));
 rootnode->data = x;
 tree = rootnode; //임시 노드로 가리킴

 node* leftnode; //왼쪽 부터니까 left노드 생성하여 연결
 leftnode = (node*)malloc(sizeof(node));
 leftnode->data = y;
 rootnode->left = leftnode;
 if (y != 0) // 0이 아닐 경우 재귀 실행
 {
  add_node(tree->left); // 만약 5 3 9라면 바로 3에서 이 함수 실행 함수 내에서 같은 3인지 체크 후 노드 생성
 }

 node* rightnode;//같은 맥락
 rightnode = (node*)malloc(sizeof(node));
 rightnode->data = z;
 rootnode->right = rightnode;
 if (z != 0)
 {
  add_node(tree->right);
 }

 scanf("%d", &m);//탐색횟수 입력
 getchar();

 for (int i = 0; i < m; i++)
 {
  search(tree); //탐색 실행
 }

 return;
}

void add_node(node *L) //*재귀실행 함수*
{
 int x, y, z;
 scanf("%d %d %d", &x, &y, &z);
 getchar();

 if (x != L->data) //즉 main에서 입력된 값이나 그 후에 입력된 값이 5 3 9의 경우 3이 제대로 입력되었는지 확인
 {
  printf("error\n");
 }

 node* leftnode;
 leftnode = (node*)malloc(sizeof(node)); //main과 똑같이 동적 생성 후 값 넣고 재귀 실행 체크
 leftnode->data = y;
 L->left = leftnode;
 if (y != 0) //만약 0이라면 이어지는 노드가 없기 때문에 전 재귀로 반환
 {
  add_node(L->left);
 }

 node* rightnode;
 rightnode = (node*)malloc(sizeof(node));
 rightnode->data = z;
 L->right = rightnode;
 if (z != 0)
 {
  add_node(L->right);
 }
 return;
}

void search(node* L) 
{
 node* temp; //임시 노드 포인터 생성
 char arr[100]; 
 int length;
 scanf("%s", arr);
 getchar();

 length = strlen(arr);

 temp = L;

 printf("%d", temp->data); // 처음 뿌리 노드 출력(뿌리부터 시작하기 때문에)

 for (int i = 0; i < length; i++)
 {
  if (arr[i] == 'L')//이후 입려된 값 체크 하여 값 출력
  {
   temp = temp->left;
   printf("%d", temp->data);
  }
  if (arr[i] == 'R')
  {
   temp = temp->right;
   printf("%d", temp->data);
  }
 }
 printf("\n");

 return;
}

이진트리를 만들며 복습해보았는데 검색중에 내 코드보다 깔끔하게 재귀함수로 구현한 코드가 있어서 그걸 조금 섞어서 만들어 봤다.

확실하게 내껄로 만들기 위해서 여러번 복습해야할것 같다.